This post is thinking in progress. I’d love feedback.
How we are educated to become problem solvers
We learn problem-solving by looking at problems that have solutions. This is how our success at problem-solving is measured in school. If we’re lucky we can look in the back of the textbook for the answers, and figure out how to work towards them. This cuts problems in half, like starting to dig a tunnel at each end and hoping to meet in the middle. Starting from a question and an answer we’re simply filling in a method to get between the two. If we do well at this we call ourselves ‘problem solvers’ on our CV..
What are Bongard problems?
Mikhail Bongard invented visual pattern matching problems that reverse the normal style of the problem to be solved. We usually have a question and the answer needs to be found.
Bongard problems give you the answers, and you need to figure out “what’s the question here?”, “What’s happening?”.
From Wikipedia
The idea of a Bongard problem is to present two sets of relatively simple diagrams, say A and B. All the diagrams from set A have a common factor or attribute, which is lacking in all the diagrams of set B. The problem is to find, or to formulate, convincingly, the common factor
From Godel, Escher, Bach
When looking at Bongard problems, we can look at the solutions to previous problems and build a list of potential answers to search through, as in the example below.
How did we get here, and where are we going?
Bongard problems ask – how did we get here? This is a significant difference to normal problem solving, but it gets better.
Working in a complicated domain, such as fixing problems in IT systems, we’re often asking “what needed to happen for this problem to occur”? Knowing this, fixing the issue is relatively straightforward, but not always easy. Things can still get very complicated, but it’s all potentially knowable.
Working in a complex domain (listen to Dave Snowden talk about complexity), which means any time when people are involved, what happened last time we did X may not have the same results this time.
So in complex domains, why do we even care how we got here? I’d suggest because understanding how we got here may help us understand how the system we’re looking at is disposed to behave and because the modelling will require us to think hard about the issues (I can’t find a source for this).
How do we think hard about Bongard problems?
Bongard problems obey Occam’s Razor – “among competing hypotheses, the one with the fewest assumptions should be selected or when you have two competing theories that make exactly the same predictions, the simpler one is the better.” (https://en.wikipedia.org/wiki/Occam%27s_razor)
Douglas R Hofstadter describes a process for solving Bogard problems in the epic book Godel, Escher, Bach. (Godel, Escher, Bach: An Eternal Golden Braid, Basic Books, Inc. New York, NY, USA ©1979 p646)
Bongard problem solving would have several stages in which raw data gradually gets converted to descriptions.
- Raw data preprocessed
- some salient features are detected
- The names constitute a mini vocabulary
- Drawn from a salient feature vocabulary
- line, segment, curve, horizontal, vertical, black, white, big, small, pointy, round.
- Second stage of preprocessing
- Triangle, circle, square, indentation, protrusion, right angle, vertex, cusp, arrow
- Now the picture is ‘understood’ to some extent tentative descriptions are made
- above, below, to the right of, to the left of, inside, outside, close to, far, parallel, perpendicular, in a row, scattered, evenly spaced, irregularly spaced
- Numerical descriptors
- More complicated descriptors
- further to the right, less close to, almost parallel to
Hofstadter introduces an idea of a “description schema” or “templates” and the idea of “Sam” – a sameness director to help to solve Bongard Problems.
This is where I am. I think it’s possible to create a useful description schema or Sam for our real-life problems, using the systems approaches I’ve written about elsewhere on this blog.
Description schemas are types of weighted directed graphs, similar to the graphs used behind online recommendation engines. I’ve got a new job involving ontologies and graphs. Thanks for Ivo (@kvistgaard ) and Julian (@julianfej )for help getting started with the ideas behind linked data. More work to come here.

!["The Men in the Moon: or, the 'Devil to pay.' With thirteen cuts [by George Cruikshank], etc. [A satirical poem-chiefly in reference to the proceedings of Messrs Cobbett, Hunt, and others.]" "The Men in the Moon: or, the 'Devil to pay.' With thirteen cuts [by George Cruikshank], etc. [A satirical poem-chiefly in reference to the proceedings of Messrs Cobbett, Hunt, and others.]"](https://maketenlouder.files.wordpress.com/2018/01/11220755663_19e3d733d1_b.jpg?w=447&h=311)
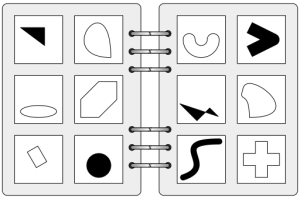 An example Bongard problem, the common factor of the left set being convex shapes (the right set are instead all concave).
An example Bongard problem, the common factor of the left set being convex shapes (the right set are instead all concave).
